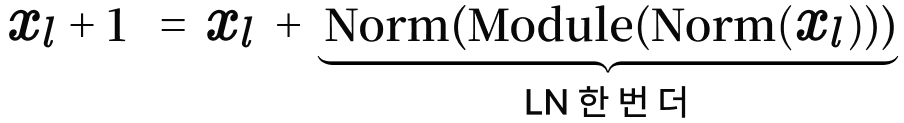개관
본 콘텐츠에서는 2025년도 ICML에서 발표된 네이버클라우드의 논문 ‘Peri-LN: Revisiting Normalization Layer in the Transformer Architecture’를 소개합니다.
과거 V100 GPU 환경에서는 왜 대규모 LLM 학습이 더 불안정했을까?
V100 GPU는 FP16(16비트 부동 소수점) 정밀도만 지원했기 때문에 학습 중 모델이 조금만 흔들려도 Loss 값이 급격히 치솟고, NaN(계산 불능)으로 발산하는 경우가 많았습니다. 당시 연구자들은 “학습이 실패하지 않을까?” 하는 불안에 시달렸습니다.
OPT 로그북이 보여주는 실제 사례
메타가 공개한 OPT-175B 로그북에 따르면, 학습 9일 차에만 40회 재시작을 했고, 1,024개의 GPU 중 하루에도 두세 대가 다운되는 등 어려움이 많았습니다. 특히 Loss 급등과 그래디언트 폭발이 반복적으로 발생했으며, 대부분은 Pre-LN 구조와 FP16 조합에서 일어났습니다.
“손실이 몇 차례나 급등하여 타격을 심하게 받았고 이를 복구하기 위해서는 학습률을 낮춰야 했습니다. (We observed several catastrophic spikes and had to lower the learning rate to recover.)” — OPT 로그북
이 글의 마지막에서는 이러한 문제가 왜 발생했는지 다시 한번 살펴보겠습니다.
Normalization Layer는 Transformer 안 어디에 있을까?
Transformer 구조에서는 모델 학습과 정보 처리를 안정화하기 위해 정규화 층(Normalization Layer)을 사용합니다. 대표적으로 LayerNorm과 RMSNorm (Root Mean Square Layer Normalization) 두 가지 방식이 있으며, 이 글에서는 이러한 정규화 층을 줄여서 LN이라 부르겠습니다.
요즘 대부분의 오픈소스 LLM 모델은 Pre-LN 구조를 기본값으로 사용하는데요, LN이 어디에 위치하느냐에 따라 훈련 난이도와 안정성이 극적으로 달라집니다.
- Post-LN은 2017년에 Transformer가 개발되었을 때 사용된 초기 안정화 방식으로, 연산이 끝난 후 히든 스테이트를 정리해 모델이 흔들리지 않도록 돕습니다.
- Pre-LN은 Llama, Qwen, Mistral, DeepSeek 등 최신 오픈소스 LLM들이 채택한 구조로, 연산 전에 입력을 먼저 안정화해 학습이 더 안정적으로 진행되도록 합니다.
Peri-LN 등장 배경
과거에는 LN을 어디에 배치하느냐에 따라 Transformer의 안정성과 성능이 달라진다는 점이 밝혀지며, Pre-LN과 Post-LN 구조가 활발히 연구되었습니다.
하지만 최근 공개된 Gemma2, Gemma3, Olmo2 등 주요 오픈소스 모델들은 기존과는 다른 새로운 LN 배치 구조를 사용하기 시작했습니다. 이처럼 아직 명확한 이름이 없던 구조를 이번 연구에서는 Peri-LN이라 명명하고, 그 구조적 특징과 성능상의 이점을 분석합니다. (참고로 ‘peri-’는 영어로 ‘~의 주위에’를 의미하는 접두어입니다.)
Peri-LN은 기존 Pre-LN 구조에서 모듈 출력에도 LN을 추가한 방식으로, 연산의 입력과 출력 양쪽 모두를 정규화합니다. Gemma2와 Gemma3, Olmo2 등 최근 등장한 주요 모델들이 이 구조를 채택하고 있다는 점에서 그 가능성에 주목할 필요가 있습니다. LN은 신호의 분산을 제한해 안정적인 학습 흐름을 유지하게 해주는 장치입니다. 그렇다면 Peri-LN은 기존의 Pre-LN과 Post-LN에 비해 어떤 차별점과 특징을 갖고, 어떤 목적으로 설계되었을까요? 다음 섹션에서 자세히 살펴보겠습니다.
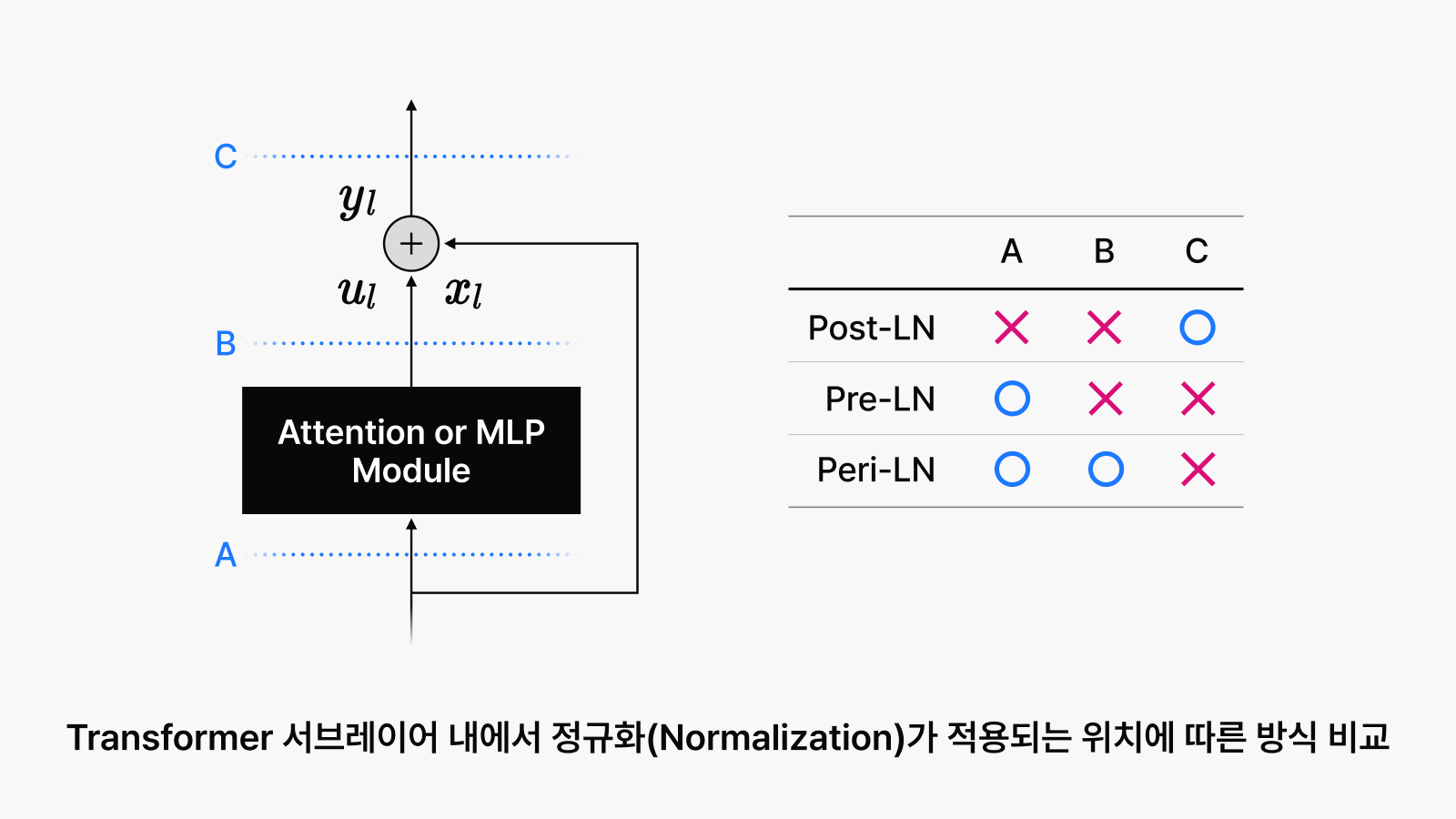그림 1. Transformer 서브레이어 내에서 정규화 적용 위치에 따른 방식 비교
히든 스테이트 분산
히든 스테이트란?
Transformer에서는 각 레이어가 끝날 때마다 d-차원의 벡터, 즉 히든 스테이트가 생성됩니다. 층이 쌓일수록 이 벡터들이 이어지며, 모델이 문맥과 의미를 이해하고 처리하는 데 필요한 정보를 구성합니다. 여기서 중요한 건 히든 스테이트의 분산(Variance)입니다. 이 값이 지나치게 빨리 커지면 모델 학습이 중간에 불안정해질 수 있습니다. 반대로 분산이 잘 제어되면, 학습이 끝까지 안정적으로 이어집니다. 즉, 분산이 얼마나 빠르게 커지느냐는 학습 성공 여부를 가르는 핵심 지표가 되는 것이죠.
아래에서는 초기화와 학습 중 두 관점에서 세 가지 LN 전략을 비교해 보겠습니다.
초기화 단계의 이론적 분석: ‘시동을 켜기 전’
초기화 단계란, 학습을 시작하기 전 모델의 파라미터가 무작위 값으로만 채워져 있는 상태입니다. 이때 세 가지 LN 구조의 분산 패턴은 다음과 같습니다.
- Post-LN: 분산이 거의 일정하게 유지됩니다.
- Pre-LN: 분산이 선형적으로 증가합니다. 단, 실제 학습 시에는이보다 더 복잡한 변화가 일어납니다.
- Peri-LN: Pre-LN과 마찬가지로 분산이 선형 증가합니다.
기존 연구는 대부분 이 초기화 시점, 즉 정적인 분석에만 집중해 왔습니다. 그래서 Pre-LN과 Peri-LN이 비슷해 보였습니다. 하지만 최근에는 학습이 끝난 모델에서 뒤에서 설명할 Massive Activation 현상이 발견되며, 학습 과정 전체를 살펴보는 시각이 필요하다는 점이 주목받고 있습니다. (논문 참조)
과연 학습 초기화 단계와 학습이 완료된 단계 사이에서는 어떤 일이 일어나고 있었던 것일까요? 초기화 단계 분석만으로는 훈련 과정에서 벌어지는 동적 현상을 놓치기 쉽습니다. 결국 실전에서 안정적인 학습을 논하려면 단순한 초깃값 분석만으로는 부족하며, 학습 전반의 동적인 변화를 추적하는 관점이 필수입니다.
학습이 시작되면 벌어지는 일: ‘엔진에 연료를 넣고 페달을 밟는 순간’
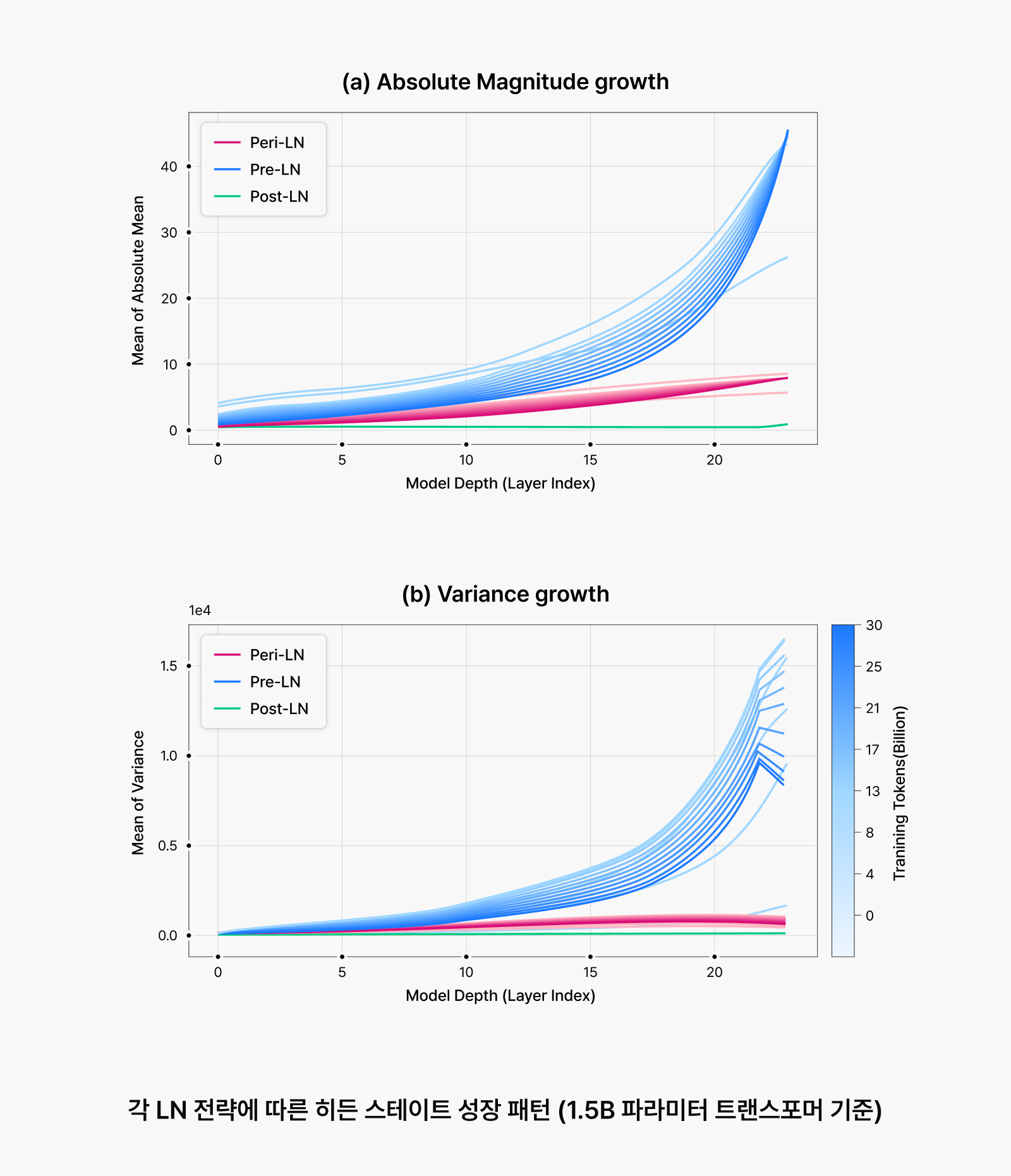
그림 2. 트랜스포머(1.5B 파라미터)에서 각 LN 구조별 히든 스테이트 증가 양상
모델 학습이 본격적으로 시작되면, 무작위였던 파라미터가 조금씩 업데이트되기 시작합니다. 마치 자동차에 연료를 넣고 엑셀을 밟는 순간처럼, 본격적인 변화가 일어나는 시점이죠. 이때 LN 구조에 따라 히든 스테이트의 분산과 그래디언트 흐름에 큰 차이가 생깁니다:
- Pre-LN: 초기에는 선형으로 증가하던 분산이 학습 초반부터 지수적으로 폭증하며, 소위 Massive Activation 현상을 유발합니다.
- Post-LN: 분산은 잘 억제되지만, 대신 그래디언트가 작아져 깊은 층까지 신호가 제대로 전달되지 않습니다. 그 결과, 하위 레이어가 사실상 학습에서 소외됩니다.
- Peri-LN: 분산과 그래디언트 사이의 균형을 잡아, 두 문제를 모두 완화해 줍니다.
💡 Tip. 히든 스테이트의 분산이 너무 커지면, 신호에 비해 잡음이 커져 Optimizer가 방향 감각을 잃습니다.
이럴 땐 ‘어디를 얼마나 학습해야 할지’ 모델이 제대로 판단하지 못해 Loss가 갑자기 치솟거나 그래디언트가 폭발하고, 심하면 아예 학습이 발산될 수 있습니다. Peri-LN은 바로 이 위험 구간을 효과적으로 누그러뜨릴 수 있는 구조로 작동합니다.
수식으로 살펴보기
왜 이렇게 차이가 날까?
- Pre-LN 구조에서는 레이어마다 히든 벡터의 크기가 점점 커지는 양방향 루프가 형성됩니다.
- Peri-LN은 출력에도 정규화를 걸어 그 루프를 끊어냅니다.
그래서 같은 학습률과 가중치 증가 폭이어도, Peri-LN은 분산 증가가 억제되고 학습이 안정적으로 진행됩니다.
1. Pre-LN
Pre-LN 구조에서는 다음과 같은 수식이 성립합니다.
여기서 k 는 아래와 같이 정의됩니다.
즉, 입력의 분산이 (1 + k) 배씩 계속 커지게 되며, 1 + k > 1 이면 분산이 기하급수적으로 증가합니다.
2. Peri-LN
Peri-LN 구조는 다음과 같이 바뀝니다.
이때 β₀는 상수 수준의 분산을 가지므로, 분산이 선형적으로 증가합니다.
Pre-LN은 입력이 커질수록 출력도 함께 커지는 증폭 루프를 만들어 학습이 진행될수록 분산이 폭주할 위험이 있는 반면, Peri-LN은 출력에서 한 번 더 정규화를 적용해 이 루프를 차단합니다. 그래서 같은 학습률과 가중치 증가 폭이라도 분산 궤적이 선형으로 억제되고, 전체 학습이 끝까지 안정적으로 이어질 수 있습니다.
큰 분산이 학습 불안정을 일으키는 건 아닐까?
분산이 크다고 해서 항상 학습이 실패하는 건 아닙니다. 진짜 문제는 분산과 그래디언트가 곱셈 관계로 연결되어 있다는 점입니다. Pre-LN 구조에서는 그래디언트의 크기(Norm)는 히든 스테이트의 크기에 비례하기 때문에, 히든 스테이트의 분산이 커지면 그래디언트도 함께 커져 학습이 불안정해질 수 있습니다.
반면, Peri-LN은 각 어텐션과 MLP(다층 퍼셉트론) 모듈 뒤에 LN이 추가로 적용되어, 이 곱셈 관계를 완충해 줍니다. 덕분에 분산이 크더라도 그래디언트가 폭주하지 않으며, 학습 안정성이 유지됩니다.
Pre-LN 구조의 히든 스테이트 분산 살펴보기
Pre‑LN의 한 층을 아주 단순화하면 아래와 같습니다.
여기서 모듈 출력의 분산이 커지면 x l + 1 도 그대로 커지고, 논문에서는 이를 다음처럼 표현합니다.
즉 k > 0 이면 계속 곱해지면서 기하급수로 불어난다는 뜻이죠.
더 큰 문제는 그래디언트도 히든 크기에 정비례한다는 점입니다.
⇒ 히든 벡터 ||h|| 가 커지는 순간, 그래디언트 폭발!
Peri‑LN 한 스푼 넣으면? 🪄
Peri‑LN은 앞뒤로 두 번 정규화합니다.
모듈 출력에 LN을 한 번 더 씌우면, 출력 분산이 상수 β₀ 근처로 묶여서 선형(또는 그 이하) 증가로 눌러 줍니다.
그래디언트 쪽도 마찬가지로 분모에 최종 출력인 히든 스테이트 ||a|| 가 들어가 자동 완충이 걸립니다.
학습 안정성
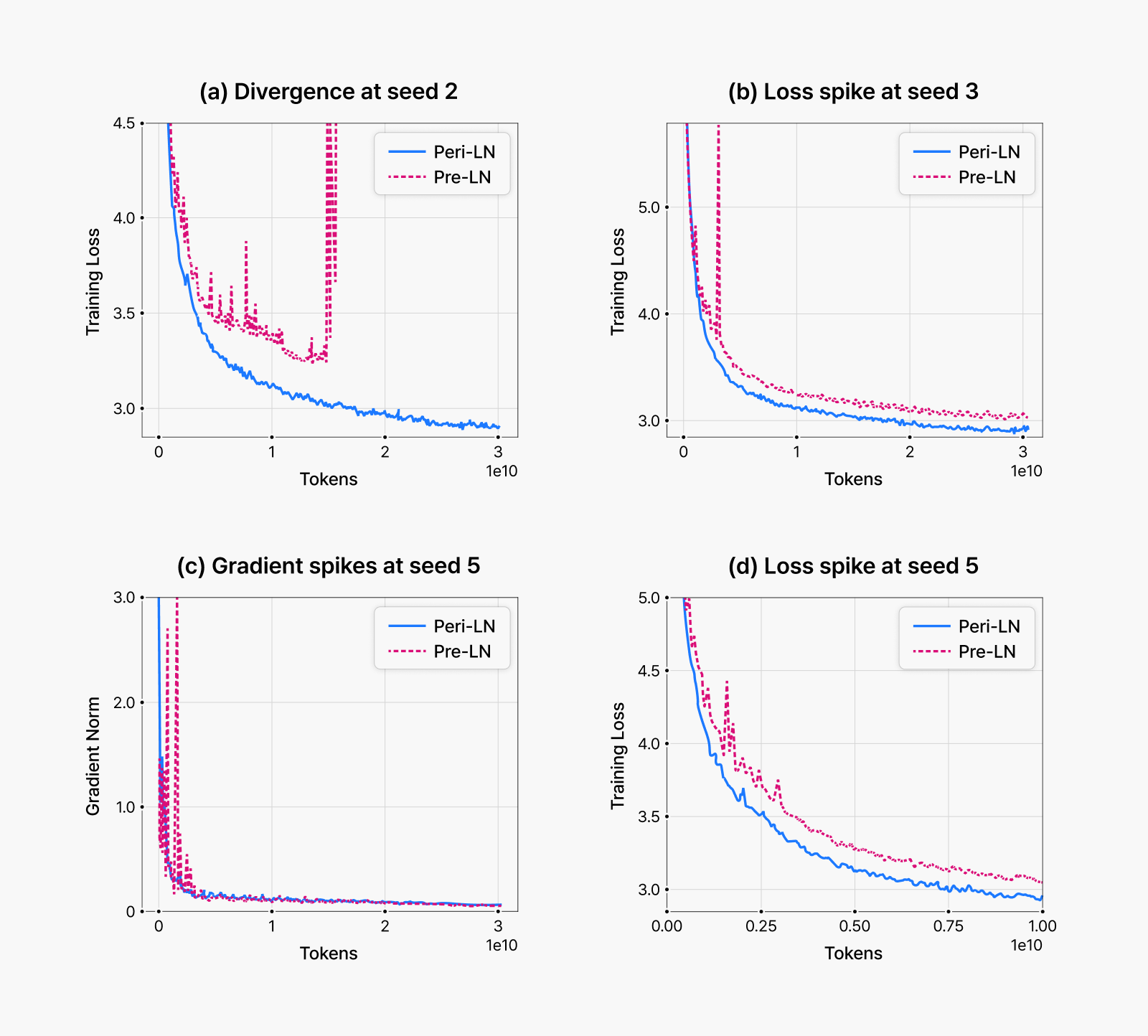
아래 그림에서 볼 수 있듯이, 대규모 LLM 사전 학습 중에는 Pre-LN 구조의 불안정성이 쉽게 드러납니다. 대표적으로는 Loss가 갑자기 튀는 학습 손실 스파이크, 그래디언트 급등, 심한 경우 학습 발산까지도 자주 관찰됩니다. 반면, Peri-LN 구조는 동일한 조건에서도 이러한 불안정한 현상이 거의 나타나지 않았으며, 전반적으로 훨씬 안정적인 학습 곡선을 유지했습니다.
그림 3. 사전 학습 초기 단계에서 흔히 발생하는 불안정성 사례. 여러 실험에서 다양한 무작위 시드(seed)를 적용해 본 결과, Pre-LN 구조는 학습 초반에 불안정한 현상을 자주 보였습니다. 처음에는 학습률이 너무 높아서 그런 것이 아닐지 의심했지만, 학습률을 낮춰도 문제가 크게 개선되지는 않았습니다. 반면 Peri-LN 구조는 동일한 설정에서도 훨씬 안정적인 학습 곡선을 보여주었습니다. (a), (b), (c)는 파라미터 수가 4억 개인 모델에서의 결과이며, (d)는 15억 개 파라미터 모델에서의 결과를 나타냅니다.
Massive Activation이 정말 학습 불안정성을 야기할까?
가중치 감쇠(Weight Decay)는 학습 과정에서 파라미터의 크기를 일정 수준으로 유지해주는 정규화 기법으로, 학습 안정성과 밀접한 관련이 있는 것으로 알려져 있습니다. (논문 참조)
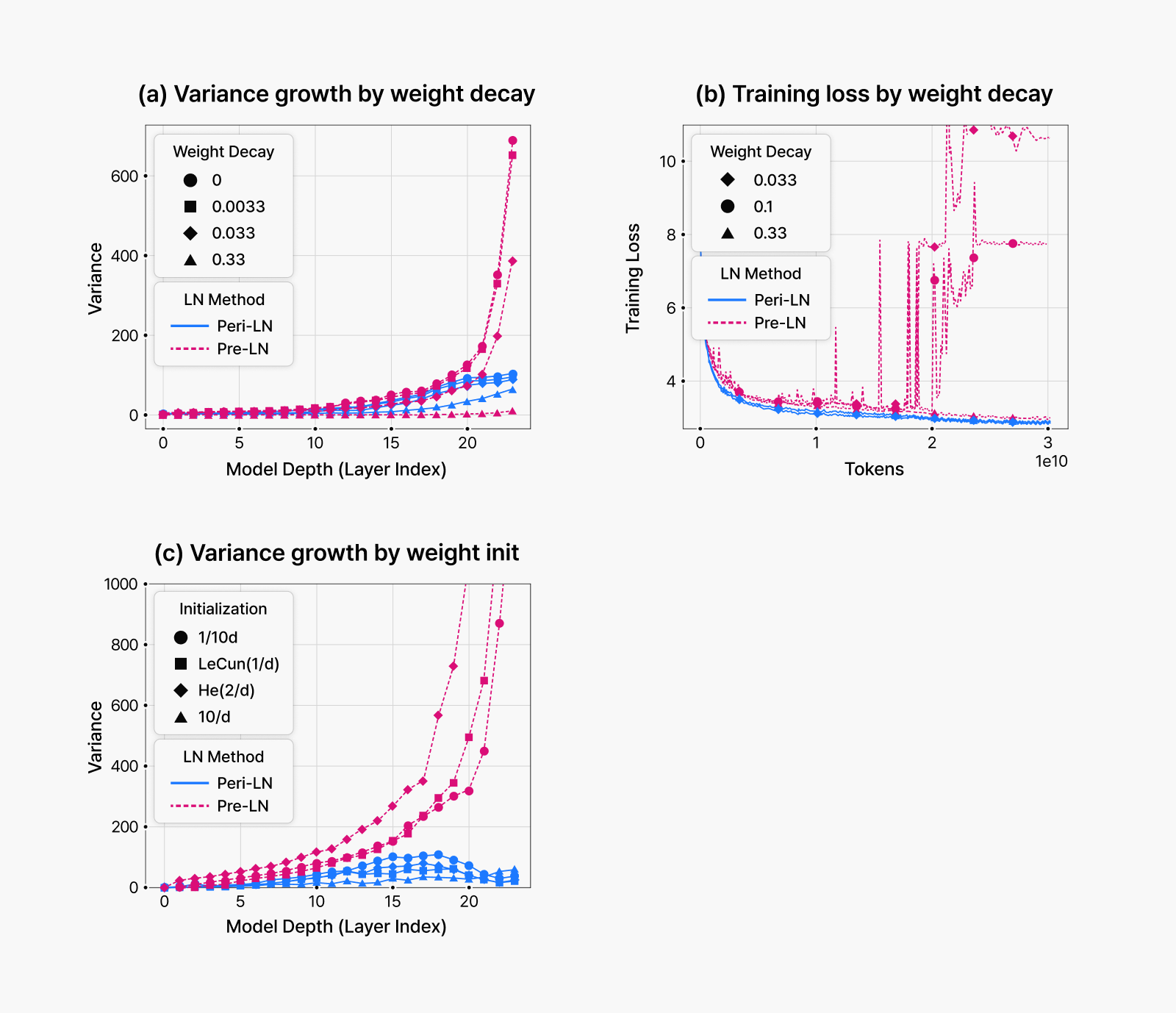
그림 4. 가중치 감쇠와 초기화가 Massive Activation에 미치는 영향
그림 4(a)에서 보이듯, 가중치 감쇠를 적용하면 Massive Activation을 억제할 수 있다는 사실을 확인했습니다. 특히 Pre-LN 구조에서는 매우 큰 가중치 감쇠 계수를 적용함으로써 Massive Activation을 효과적으로 제거할 수 있었습니다.
이러한 실험 결과는 앞서 제시한 ‘큰 히든 스테이트가 그래디언트 불안정성을 유발한다’는 결론과 연결됩니다. 이를 더 분명히 검증하기 위해, Massive Activation이 실제로 학습 불안정성을 유발하는지 확인하는 추가 실험을 진행했습니다. 방법은 다음과 같습니다. 기존에는 학습이 중간에 발산했던 설정에 대해 강한 가중치 감쇠를 적용하여 Massive Activation을 억제한 후, 학습이 안정화되는지를 관찰했습니다.
그림 4(b)에서 보이듯이 Massive Activation이 제거되자 학습이 안정적으로 진행되었습니다. 즉, 실험을 통해서 히든 스테이트가 과도하게 크면 (Massive Activation이 발생하면) 그래디언트 불안정성으로 이어진다는 것을 입증했습니다.
Normalization Layer 구조별 성능 벤치마크
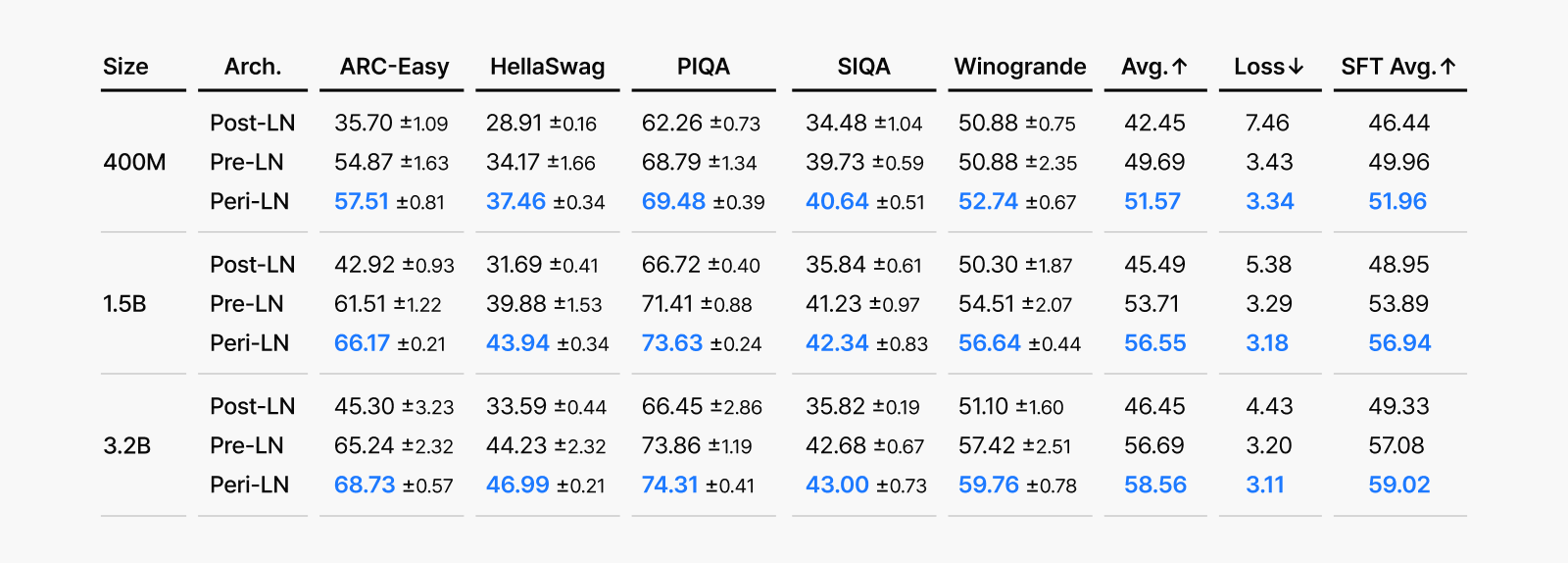
Post-LN, Pre-LN, Peri-LN 구조를 각각 적용한 트랜스포머 모델들을 주요 벤치마크에서 비교한 결과, Peri-LN은 항상 가장 안정적이고 우수한 성능을 기록했습니다. 모델 크기에 상관없이, 그리고 여러 번 반복한 학습 실험에서도 Peri-LN은 편차가 적고 일관된 결과를 보여주었죠. 이는 단순히 최종 성능이 높을 뿐 아니라, 어떤 환경에서 학습하더라도 기대할 수 있는 성능이 가장 높은 구조임을 의미합니다.
그림 5. Post-LN, Pre-LN, Peri-LN 세 가지 정규화 구조를 가진 LLM이 서로 다른 크기(400M/1.5B/3.2B)로 훈련했을 때, 다양한 벤치마크 과제에서 어떤 성능을 보였는지를 비교한 결과. 각 점수는 5개의 다른 무작위 시드로 학습한 평균값과 표준편차로 표시
왜 Pre-LN은 FP16에서 더 위험할까?
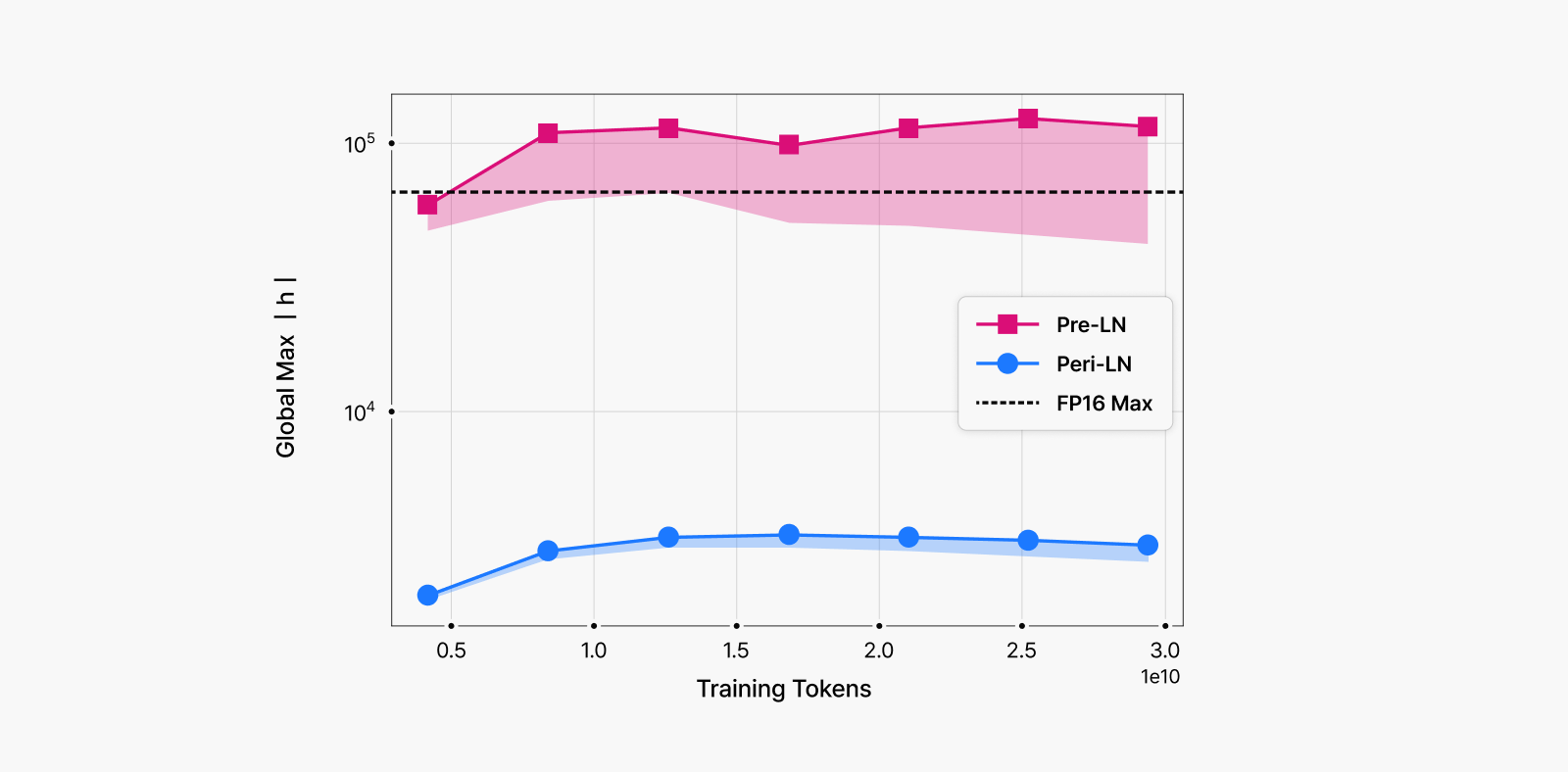
그림 6. 학습 과정에서 히든 스테이트의 절댓값이 얼마나 크게 튀는지 관찰한 그래프
그래프에 표시된 색 띠는 상위 100개의 절댓값 활성화 범위를 보여줍니다.
- Pre-LN(빨간색)은 학습이 진행될수록 빠르게 증가하며, FP16이 표현할 수 있는 수치의 한계(주황색 점선)를 초과해 버립니다.
- Peri-LN(파란색)은 전체 학습 내내 이 한계치 아래에서 안정적으로 유지됩니다.
즉, Peri-LN은 히든 스테이트가 과도하게 커지는 현상(Massive Activation)을 효과적으로 억제한다는 점을 시각적으로 보여줍니다.
이제 다시 처음에 던졌던 질문으로 돌아가 봅니다. 과거 V100 GPU 환경에서는 왜 대규모 LLM 학습이 더 불안정했을까?
앞서 설명했듯이 Pre-LN 구조에서는 모델 규모가 커질수록 깊은 층에서 점점 더 큰 히든 스테이트가 발생합니다. 이 값들이 정규화 없이 누적되면, 특히 3B 파라미터 규모 이상의 모델에서는 FP16 포맷이 표현할 수 있는 최대 수치를 쉽게 넘어버리게 됩니다 (그림 6). 이러한 히든 스테이트의 폭주가 그대로 이어지면, 학습 중 Loss 스파이크나 발산과 같은 심각한 불안정성으로 직결됩니다. 실제로 OPT 학습 로그에서도 이러한 현상이 다수 보고된 바 있습니다.
물론 현재는 A100 이상의 GPU에서 지원되는 BF16 포맷 덕분에 이 문제를 어느 정도 해결할 수 있습니다. 하지만 FP16 포맷을 계속 사용할 경우, 동일한 불안정성 문제가 재현될 수 있습니다. 이러한 이유로, 오늘날에도 FP16 환경에서는 학습 뿐 아니라 추론 단계에서도 불안정성 차이가 발생하며, 이는 FP16과 BF16의 실사용 성능 차이로 이어지기도 합니다.
맺으며
이번 연구에서는 새로운 트랜스포머 구조인 Peri-LN에 대한 분석과 기존 Pre-LN 구조의 학습 불안정성의 원인을 파악하는 내용을 살펴보았습니다. 모델을 더 크게 만드는 일만큼, 안전하게 키우는 일도 중요합니다. Peri-LN은 안전벨트를 한 번 더 착용해, 거대한 언어 모델도 안전하게 학습될 수 있도록 돕습니다. LLM 학습 시 불안정성이 걱정된다면 Peri-LN 구조를 채택해 보는 것은 어떨까요?
이번 연구 여정을 통해 우리는 ‘서비스와 연구는 결코 독립된 평행선이 아니다’라는 사실을 체감했습니다. 실무에서 만난 문제(학습 불안정성)는 곧바로 연구 질문이 되었고, 연구로 정제된 통찰은 다시 프로덕션 코드에 녹아들어 서비스 지표를 끌어올렸습니다. 현장 문제를 이론으로 해석하면 ‘왜’가 분명해지고, 검증된 이론을 제품에 적용하면 ‘어떻게’가 빨라짐을 느꼈습니다.
연구와 프로덕션의 탄탄한 브리지 역할이야말로 대규모 LLM 생태계에 필요한 또 하나의 안전장치라 믿습니다. 앞으로도 서비스에서 발견한 질문을 연구로 확장하고, 연구에서 얻은 해답을 제품으로 환원하며, 두 영역을 잇는 다리를 단단히 놓아가겠습니다.
자세한 연구 내용은 논문 전문에서 확인하실 수 있습니다.